【VR課堂 3D優課】高中數學《空間兩點間的距離公式》

人教版  高中《數學2》第四章

 4.3.2《空間兩點間的距離公式》

【教學目標】

1、 掌握空間中兩點間距離的計算公式

2、 學習如何計算空間點到原點的距離

【教學重點與難點】

重點：空間中兩點間距離的計算公式

難點：空間中兩點間距離的計算公式的推導

【教學過程】

1.     復習引入（10分鐘）

（1）    【老師】復習勾股定理公式：設直角三角形兩直角邊為a和b，斜邊為c

【學生】 a2+b2=c2

（2）    【老師】復習在平面上任意兩點A (x₁，y₁)，B (x₂，y₂)之間的距離的公式

【學生】

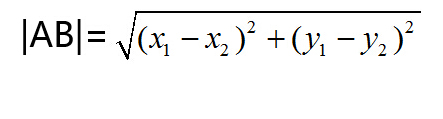
（3）    【老師】提問：那么對于空間中任意兩點A (x₁，y₁，z₁₎，B (x₂，y₂，z₂)之間的距離的公式會是怎樣呢？現實生活中什么情況下需要計算空間中任意兩點間的距離呢？只需引導學生大膽猜測，是否正確無關緊要。

     【學生】踴躍回答

2.     新課教學（25分鐘）

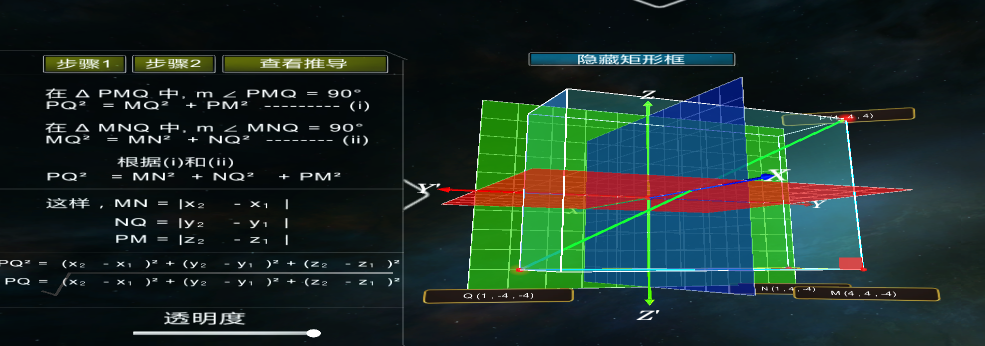
（1）演示環節：推導空間兩點間距離公式

觀看VR/3D教學視頻，學生可從演示視頻中了解以下信息

A．本節課的學習目標

B．現實生活中空間兩點距離計算的應用

C．演示空間兩點距離公式的推導過程（教師可以配合視頻講解公式推導過程）

a.確定空間任意兩點P(x₁，y₁，z₁), Q(x₂，y₂，z₂)

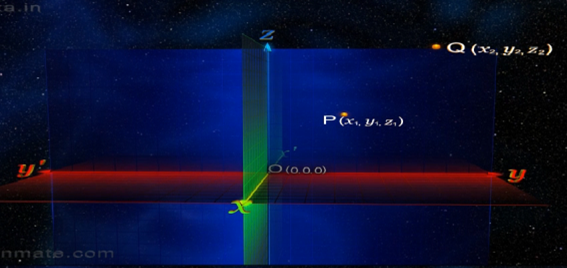
b.直線PL與直線QM垂直于平面XOY，

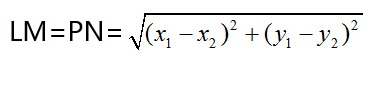
c.QN=QM-QN=QM-PL=z₂-z₁

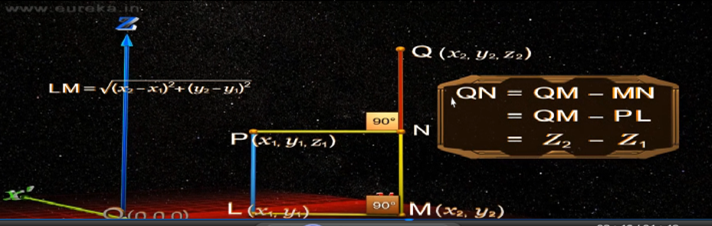
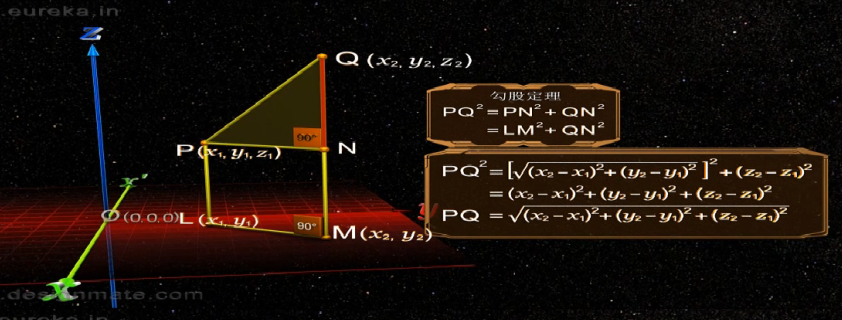
d.根據勾股定理, PQ²=PN²+QN²=LM²+QN²

       e.

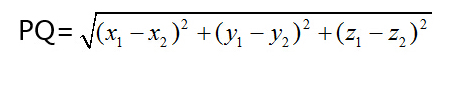
f． 根據公式，推出任意一點(x，y，z)與原點（0,0,0）的距離公式為

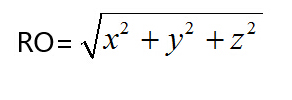
（2）互動環節：教師打開3D教學互動模塊，與學生一起分步驟推導空間兩點間距離公式，調動課堂氣氛，引導學生思考，加深學生對公式推導過程的理解。

（3）練習環節：教師用鼠標任意拖動PQ兩點在任意位置上，要求學生利用公式計

算PQ兩點間的距離。可以用個別提問方式，或小組比賽方式進行。

3.     書本練習（10分鐘）

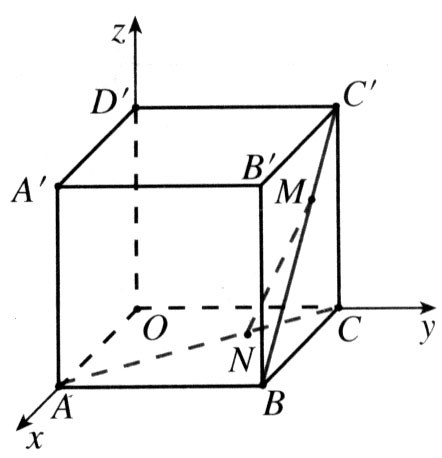
詳見138頁練習第4題：如圖，正方體棱長為a，AN=2CN,BM=2MC’,求MN長。