【教學目標】
一、理解對數的概念,了解對數與指數的關系;掌握對數式與指數式的互化;理解對數的性質,掌握以上知識并形成技能.
二、通過實例使學生認識對數模型,體會引入對數的必要性;通過師生觀察分析得出對數的概念及對數式與指數式的互化.
三、通過學生分組進行探究活動,掌握對數的重要性質.通過做練習,使學生感受到理論與實踐的統一.
四、培養學生的類比、分析、歸納能力,培養學生嚴謹的思維品質以及在學習過程中培養學生的探究意識.
【重點與難點】
重點:1.對數的概念;2.對數式與指數式的相互轉化.
難點:1.對數概念的理解;2.對數性質的理解.
【教學過程】
一、引入新課
1.一尺之錘,日取其半,萬世不竭.
(1)取5次,還有多長?
(2)取多少次,還有0.125尺?
分析:
(1)為同學們熟悉的指數函數模型,易得(1/2)5=1/32,
(2)可設取x次,則有(1/2)x=0.125,
(3)抽象出:(1/2)x=0.125?x=?
2.2002年我國GDP為a億元,如果每年平均增長8%,那么經過多少年GDP是2002年的2倍?
分析:設經過x年,則有(1+8%)x=2,抽象出:(1+8%)x=2?x=?
二、講授新課
1.對數的概念(3分鐘)
一般地,如果ax=N(a>0,且a≠1),那么數x叫做以a為底N的對數(logarithm),記作x=logaN,其中a叫做對數的底數,N叫做真數.
注意:(1)底數的限制:a>0且a≠1;
(2)對數的書寫格式.
2.對數式與指數式的互化:(5分鐘)
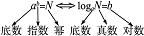
冪底數←a→對數底數
指數←b→對數
冪←N→真數
思考:
(1)為什么對數的定義中要求底數a>0且a≠1?
(2)是否是所有的實數都有對數呢?
負數和零沒有對數
3.兩個重要對數(2分鐘)
(1)常用對數:以10為底的對數log10N,簡記為lg N;
(2)自然對數:以無理數e=2.718 28…為底的對數logeN,簡記為lnN.(在科學技術中,常常使用以e為底的對數)
注意:兩個重要對數的書寫
4.對數的性質(12分鐘)
探究活動1
求下列各式的值:
(1)log31=0;(2)lg 1=0;
(3)log0.51=0;(4)ln1=0.
思考:你發現了什么?
“1”的對數等于零,即loga1=0(a>0且a≠1),類比:a0=1(a>0且a≠1).
探究活動2
求下列各式的值:
(1)log33=1;(2)lg 10=1;(3)log0.50.5=1;(4)lne=1.
思考:你發現了什么?
底數的對數等于“1”,即logaa=1(a>0且a≠1),類比:a1=a(a>0且a≠1).
探究活動3
求下列各式的值:
(1)![]() =3;(2)
=3;(2)![]() =0.6;(3)
=0.6;(3)![]() =89.
=89.
思考:你發現了什么?
對數恒等式:![]() =N(a>0且a≠1).
=N(a>0且a≠1).
探究活動4
求下列各式的值:
(1)log334=4;(2)log0.90.95=5;(3)lne8=8.
思考:你發現了什么?
對數恒等式:logaan=n(a>0且a≠1).
5.小結(12分鐘)
(1)播放VR/3D教學資源:高中數學-代數-指數與對數,結合上節課關于指數的內容,總結指數與對數之間的關系。

(2)負數和零沒有對數;
(3)“1”的對數等于零,即loga1=0;
(4)底數的對數等于“1”,即logaa=1;
(5)對數恒等式:![]() =N;
=N;
(6)對數恒等式:logaan=n.(a>0且a≠1)
6.布置作業
課本習題2.2A組第1,2題.