【教學目標】
知識與技能:
使學生理解因數和倍數的意義,會判斷一個數是不是另一個數的因數或倍數。
過程與方法:
通過實驗,猜測,驗證,總結等活動,掌握因數和倍數的概念,發現因數和倍數的關系,總結出求一個數的因數和倍數的方法。
情感態度與價值觀:
培養學生抽象、概括的能力,滲透事物之間相互聯系、相互依存的辯證唯物主義的觀點。以及學生的合作意識、探索意識,以及熱愛數學學習的情感。
【教學重點與難點】
重點:通過實驗,猜測,驗證,掌握因數和倍數的概念,發現因數和倍數的關系,總結出求
一個數的因數和倍數的方法。
難點:發現并且總結出因數和倍數的關系,以及求一個數的因數和倍數的方法。
【教學準備】
課件、練習紙、云幻科教VR/3D教學資源。
【教學過程】
一、創設情境,引入新課
師:人與人之間存在著許多種關系,你們和爸爸(媽媽)的關系是……?
生:父子(父母、母子、母女)關系。
師:我和你們的關系是……?
生:師生關系。
師:對,我是你們的老師,你們是我的學生,我們的關系是師生關系。在數學中,數與數之間也存在著多種關系,這一節課,我們一起探討兩數之間的因數與倍數關系。
板書課題:(因數和倍數)
二、舉例交流,引入新知
師:我們已經認識了哪幾類數?
生:自然數,小數,分數。
師:現在我們來研究自然數中數與數之間的關系。下面我們來看一下下面的例題,做一做,看一看我們會發現什么。
(一)引導觀察,提出概念
1.出示教材第5頁的【例1】。
觀察下面的算式并分類。
12÷2=6 9÷5=1.8 30÷6=5
2÷4=0.5 26÷8=3.25 29÷4=7.25
20÷10=2 21÷21=1 63÷9=7
師:同學們可以分成小組討論一下,然后把討論的結果寫出來,一會跟大家說一說。
生:我們分成了這樣的兩類:
第一類:12÷2=6 30÷6=5 20÷10=2 21÷21=1 63÷9=7
第二類:9÷5=1.8 2÷4=0.5 26÷8=3.25 29÷4=7.25
師:那你可以說一說你是怎么分的嗎?
生:第一類除數的商是整數,第二類除數的商是小數。
師:是的,那這一組算式跟我們今天要學的因數和倍數有什么關系呢。什么是因數,什么是倍數呢,下面就讓老師來告訴你們答案。
(二)提出概念,深化了解
師:同學們分的很對,我們來看第一類算式,除數的商都是整數。那么我們就把這樣的算式歸歸類,提出這樣的概念:在整數除法中,如果商是整數而沒有余數,我們就說被除數是除數和商的倍數,除數和商是被除數的因數。例如:12÷2=6,我們就說12是2和6的倍數,2和6是12的因數。大家明白了嗎?那誰來說一說第一類其它算式中,誰是誰的因數?誰是誰的倍數?
生:30÷6=5 ,30是6和5的倍數,6和5是30的因數。
20÷10=2 ,20是10和2的倍數,10和2是20的因數。
21÷21=1,21是21和1的倍數,21和1 是21的因數。
63÷9=7,63是9和7的倍數,9和7是63的因數。
師:是的,那我們一直說的都是誰是誰的因數,誰是誰的倍數,這說明了什么呢?
生:說明因數和倍數是一起出現的。
師:這位同學說的很對,因數與倍數是相互依存的,因數和倍數說明的就是數與數之間在算式中的的關系。大家還要注意一點:為了方便,在研究因數和倍數的時候,我們所說的數指的是整數。(一般不包括0)
做一做VR/3D教學課件:“小學數學-數的因數”互動部分的題,同學們在做的過程中可以互相討論,看一看誰說的對,誰總結的好。哪位同學來說一說答案,并且說一下你的思考過程。(鼓勵同學舉手發言)
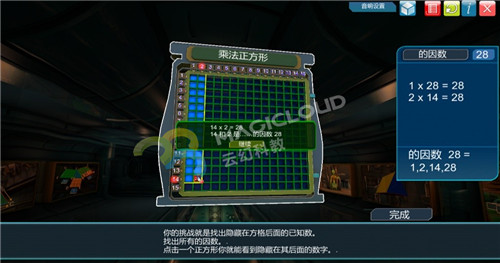
生:因為28能被1、2、14、28整除,所以1、2、14、28是28的因數,28是1、2、14、28的倍數。
如此類推運用VR/3D教學互動環節列舉5個例子,與學生共同討論因數與倍數之間的關系。
師:相信同學們都掌握了因數和倍數的概念,也知道了因數和倍數相互依存的關系。那么我們就繼續往下探討這樣一個問題,一個數的因數有幾個,一個數的倍數有哪些,它們又有什么特征呢。
(三)舉例驗證,發現總結
1.因數的個數特征
師:首先我們來看一看一個數的因數有幾個?
【例2】18的因數有哪幾個?
師:求18的因數,那就說明在18的整數除法算式里,18是被除數。那么同學們就要想一個問題了,18除以哪些整數的結果是整數呢?同學們請討論一下,給出一個完整有正確的答案。
生:18÷1=18 18÷2=9 18÷3=6
所以18的因數有1、2、3、6、9、18。
師:大家同意這個答案吧!這位同學說的很對,我們只要把所有能整除18的數找出來,就是18的因數。好的,那大家再說一說30的因數有那幾個呢?
生:30÷1=30 30÷2=15 30÷3=10 30÷5=6
30的因數有1、2、3、5、6、15、30。
師:36的因數有哪幾個呢?
生:36÷1=36 36÷2=18 36÷3=12 36÷4=9 36÷6=6
36的因數有1、2、3、4、6、9、12、18。
師:同學們找的都很對,說明大家已經理解了因數和倍數概念和它們之間的關系。那大家有沒有從這里面發現什么有意思的規律呢?
生:一個數的最小因數,是1;它的最大因數是它本身。比如18的最小因數是1,最大因數是18.
師:同學們觀察的非常仔細,說的很對。那下面我們來看一看一個數的倍數都有哪些呢?
2.倍數的個數特征
【例3】2的倍數有哪些?
師:同學們根據倍數的概念,想一想,應該怎樣找呢?
生:應該找哪些整數除以2商還是整數,例如:2÷2=1 4÷2=2 6÷2=3 8÷2=4 10÷2=5
12÷2=6……所以2的倍數有2、4、6、8、10、12……
生:因為乘法和除法是互逆的,所以還可以這樣找:2×1=2 2×2=4 2×3=6 2×4=8 2×5=10 2×6=12……這里的積都是2的倍數。
師:我想同學們在算的過程中已經發現倍數的特征了,一個數的倍數的個數是無限的。一個數的最小倍數是它本身,沒有最大倍數。對不對?
生:是的。
師:好的,那么我們再來說一說3的倍數和5的倍數,驗證一下剛才的發現。
師:3的倍數有哪些?
生:3÷3=1 6÷3=2 9÷3=3 12÷3=4 15÷3=5 18÷3=6……
3的倍數有3、6、9、12、15、18……
生:5×1=5 5×2=10 5×3=15 5×4=20 5×5=25 5×6=30……
5的倍數有5、10、15、20、25、30……
師:接下來觀看VR/3D教學視頻:小學數學-數的因數,留意視頻講述因數的特征。
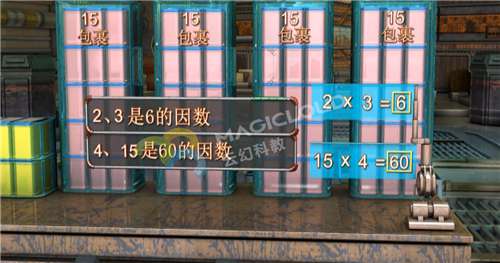
師:根據因數的特征,結合因數與倍數的關系,讓我們做以下總結:
(1)一個數的因數的個數是有限的,一個數的倍數的個數是無限的。
(2)一個數的最小因數是1,最大因數是它本身。
(3)一個數的最小倍數是它本身,沒有最大倍數。
三、及時練習,鞏固提高
師: 我們已經掌握了因數和倍數的特點,下面請同學們判斷一下下面幾道題的對與錯,并說出你的理由。
1、任何自然數,它的最大因數和最小倍數都是它本身。( )
2、一個數的倍數一定大于這個數的因數。( )
3、5是因數,10是倍數。( )
4、36的全部因數是2、3、4、6、9、12和18,共有7個。( )
5、任何一個自然數最少有兩個因數。( )
生:
1、(√)根據因數和倍數的特點,一個數的最大因數和最小倍數是它本身。例如6的最大因數和最小倍數都是6.
2、(×)例如3的最小倍數是3,最大因數也是3,它們是一樣大的。
3、(×)因為因數和倍數是相互依存的關系,所以應該說5是10的因數,10是5的倍數。
4、(×)36的因數還有1和36,所以36的因數一共有9個。
5、(×)自然數1的因數只有1本身。
四、課后小結
1.提問:這節課你都獲得了哪些知識? 在本節課中你最大的收獲是什么?
學生:了解了因數和倍數的概念,并且通過實驗和討論,發現并總結出了因數和倍數的特征。
2.教師歸納整理。
(1)首先我們學習了因數和倍數的概念。在整數除法中,如果商是整數而沒有余數,我們就說被除數是除數和商的倍數,除數和商是被除數的因數。
(2)因數和倍數是相互依存的。
(3)一個數的因數的個數是有限的,一個數的倍數的個數是無限的。
(4)一個數的最小因數是1,最大因數是它本身。
(5)一個數的最小倍數是它本身,沒有最大倍數。